안녕하세요

사회과학연구에서 구조방정식을 활용한 다양한 연구들이 주목받고 있음에 따라서 다양한 통계도구들로 구조방정식을 수행하는 연구들이 많이 지고 있는데요.
이번시간에는 무료 통계소프트웨어인 R을 활용하여 구조방정식을 해보겠습니다.
1. 구조방정식이란?
구조방정식(Structural Equation Modeling, SEM)은 관측된 변수와 잠재변수(latent variable) 간의 인과적 관계를 모델링하는 방법 중 하나입니다.
SEM은 일반적으로 구조 방정식 모델링 또는 패스 모델링으로 알려져 있습니다. 이 방법은 여러 관측 변수(예: 설문조사 항목)와 잠재변수(예: 우울증) 간의 복잡한 관계를 모델링할 수 있습니다.
구조방정식은 선형 모델링과 비선형 모델링 모두를 수행할 수 있으며, 측정모델과 구조모델로 구성됩니다. 측정모델은 관측된 변수와 잠재변수 간의 관계를 모델링하고, 구조모델은 잠재변수와 다른 잠재변수 또는 관측된 변수 간의 관계를 모델링합니다.
구조방정식은 다양한 분야에서 활용되고 있으며, 예측 모델링, 심리학, 교육, 사회과학 등 다양한 분야에서 이용되고 있습니다. SEM은 상관관계나 회귀분석보다 더 복잡한 데이터 분석 문제를 다룰 수 있는 강력한 방법입니다.
2. 구조방정식을 하기위한 2단계 접근법
확인적 요인분석(Confirmatory Factor Analysis, CFA)과 구조방정식을 활용한 2단계 접근법은 대규모 데이터셋에서 잠재변수를 모델링하고자 할 때 효과적인 방법입니다.
1단계에서는 CFA를 사용하여 측정모델을 추정합니다. 이를 위해서는 먼저 이론적으로 유의미한 잠재변수를 식별하고, 각 잠재변수에 해당하는 측정된 변수들을 선택해야 합니다. CFA는 잠재변수와 측정된 변수들 간의 구조를 검증하고, 측정된 변수들이 잠재변수를 측정하기 위해 충분한 정도로 상호 관련성을 가지는지를 확인합니다.
2단계에서는 구조방정식을 사용하여 구조모델을 추정합니다. 구조모델에서는 CFA에서 추정한 잠재변수들과 다른 잠재변수 또는 측정된 변수들 간의 관계를 모델링합니다. 이를 통해, 구조방정식을 사용하여 이론적인 가설을 검증하고, 잠재변수 간의 인과관계를 모델링할 수 있습니다.
이러한 2단계 접근법은 구조모델링의 복잡성을 줄이면서도 이론적인 가설을 검증할 수 있는 장점이 있습니다. CFA에서는 잠재변수와 측정된 변수 간의 구조를 검증하고, 구조방정식에서는 잠재변수 간의 인과관계를 모델링하여 이론적인 가설을 검증합니다. 이를 통해, 이론적인 가설을 검증하면서도 측정모델과 구조모델의 적합도를 모두 평가할 수 있습니다.
3. R을 활용한 확인적 요인분석 실습
Lavaan 패키지를 활용해서 실습을 해보겠습니다.
이번 실습에 사용될 데이터셋은 Lavaan 패키지에서 기본적으로 제공되는 HolzingerSwineford1939라는 데이터셋을 사용할 예정입니다.
먼저, Lavaan 패키지와 HolzingerSwineford1939 데이터를 불러오기 위해 다음 코드를 실행해주세요.
library(lavaan)
data(HolzingerSwineford1939)SPSS에서 파일을 따로 불러오는 방법은 아래 링크를 참고해 주세요
https://speedspeed.tistory.com/33
R에서 SPSS파일 다루기 기초
개요 이 블로그 게시물에서는 R에서 SPSS 파일을 로드하고 저장하는 기본 사항과 데이터를 보고 다중 회귀 분석을 수행하는 방법을 알아보겠습니다. SPSS(Statistical Package for the Social Sciences)는 널리
speedspeed.tistory.com
1) 모형설정
이제 CFA 모형을 설정할 차례입니다. HolzingerSwineford1939 데이터는 9개의 변수를 가지고 있습니다. 이 변수들은 세 가지 요인 (Visual, Textual, Speed)에 영향을 받는 것으로 가정하고, 이를 CFA 모형으로 설정해보겠습니다.
위 코드에서 ~은 "영향을 받는다"를 뜻하며, Visual, Textual, Speed은 각각 Visual, Textual, Speed 요인을 나타냅니다. x1부터 x9는 데이터에서 사용되는 9개의 변수를 나타냅니다.
# CFA 모형 설정
model <- 'Visual =~ x1 + x2 + x3
Textual =~ x4 + x5 + x6
Speed =~ x7 + x8 + x9'이렇게 설정하게 되면 AMOS에서 아래 화면과 같이 설정하는 것과 같습니다.

위 코드에서 ~은 "영향을 받는다"를 뜻하며, Visual, Textual, Speed은 각각 Visual, Textual, Speed 요인을 나타냅니다. x1부터 x9는 데이터에서 사용되는 9개의 변수를 나타냅니다.
# 모형 적합
fit <- cfa(model, data=HolzingerSwineford1939)적합 결과를 확인하기 위해 summary() 함수를 사용해보겠습니다.
# 결과 확인
summary(fit, standardized=TRUE, fit.measures=TRUE)HolzingerSwineford1939 데이터에 대해 CFA 모형을 적합시킨 결과는 다음과 같습니다.
lavaan 0.6-11 ended normally after 35 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 21
Number of observations 301
Model Test User Model:
Test statistic 85.306
Degrees of freedom 24
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 918.852
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.931
Tucker-Lewis Index (TLI) 0.896
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3737.745
Loglikelihood unrestricted model (H1) -3695.092
Akaike (AIC) 7517.490
Bayesian (BIC) 7595.339
Sample-size adjusted Bayesian (BIC) 7528.739
Root Mean Square Error of Approximation:
RMSEA 0.092
90 Percent confidence interval - lower 0.071
90 Percent confidence interval - upper 0.114
P-value RMSEA <= 0.05 0.001
Standardized Root Mean Square Residual:
SRMR 0.065
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Visual =~
x1 1.000 0.900 0.772
x2 0.554 0.100 5.554 0.000 0.498 0.424
x3 0.729 0.109 6.685 0.000 0.656 0.581
Textual =~
x4 1.000 0.990 0.852
x5 1.113 0.065 17.014 0.000 1.102 0.855
x6 0.926 0.055 16.703 0.000 0.917 0.838
Speed =~
x7 1.000 0.619 0.570
x8 1.180 0.165 7.152 0.000 0.731 0.723
x9 1.082 0.151 7.155 0.000 0.670 0.665
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Visual ~~
Textual 0.408 0.074 5.552 0.000 0.459 0.459
Speed 0.262 0.056 4.660 0.000 0.471 0.471
Textual ~~
Speed 0.173 0.049 3.518 0.000 0.283 0.283
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x1 0.549 0.114 4.833 0.000 0.549 0.404
.x2 1.134 0.102 11.146 0.000 1.134 0.821
.x3 0.844 0.091 9.317 0.000 0.844 0.662
.x4 0.371 0.048 7.779 0.000 0.371 0.275
.x5 0.446 0.058 7.642 0.000 0.446 0.269
.x6 0.356 0.043 8.277 0.000 0.356 0.298
.x7 0.799 0.081 9.823 0.000 0.799 0.676
.x8 0.488 0.074 6.573 0.000 0.488 0.477
.x9 0.566 0.071 8.003 0.000 0.566 0.558
Visual 0.809 0.145 5.564 0.000 1.000 1.000
Textual 0.979 0.112 8.737 0.000 1.000 1.000
Speed 0.384 0.086 4.451 0.000 1.000 1.0002) 모형적합도
조금 복잡하네요 모형적합도만 추출해서 살펴보도록합시다.
fitMeasures()함수는 모형적합도만 보여줍니다
fitMeasures(fit)결과는 다음과 같습니다.
npar fmin chisq df pvalue baseline.chisq
21.000 0.142 85.306 24.000 0.000 918.852
baseline.df baseline.pvalue cfi tli nnfi rfi
36.000 0.000 0.931 0.896 0.896 0.861
nfi pnfi ifi rni logl unrestricted.logl
0.907 0.605 0.931 0.931 -3737.745 -3695.092
aic bic ntotal bic2 rmsea rmsea.ci.lower
7517.490 7595.339 301.000 7528.739 0.092 0.071
rmsea.ci.upper rmsea.pvalue rmr rmr_nomean srmr srmr_bentler
0.114 0.001 0.082 0.082 0.065 0.065
srmr_bentler_nomean crmr crmr_nomean srmr_mplus srmr_mplus_nomean cn_05
0.065 0.073 0.073 0.065 0.065 129.490
cn_01 gfi agfi pgfi mfi ecvi
152.654 0.943 0.894 0.503 0.903 0.423
위 결과에서 모형 적합의 기준은 Chi-square 검정 결과 (p-value < 0.05)입니다. Chi-square 검정 결과는 0.000으로, 유의수준 0.05보다 작으므로 다른 적합도를 살펴봐야합니다.
적합도 지수 중 Comparative Fit Index (CFI)는 0.931, Tucker-Lewis Index (TLI)는 0.896으로, 이 값이 0.9보다 크면 모형 적합이 양호하다고 평가할 수 있습니다.
RMSEA 값은 0.092로, 0.05 이하면 좋은 모형 적합을 보이는 것으로 알려져 있습니다.
SRMR 값은 0.065로, 0.08 이하인 경우 모형 적합이 좋다고 알려져 있습니다.
이러한 결과들은 HolzingerSwineford1939 데이터에 대해 CFA 모형이 썩 양호하지는 않지만 실습데이터이니 넘어갑시다.
3) 신뢰도와 집중타당도 계산
다음으로는 CFA 모형을 적합시킨 후에는 각 요인에 대한 신뢰도 (reliability)를 평가하는 것이 일반적입니다.
아쉽게도 Lavaan은 신뢰도 계산이 안됩니다. 따라서 semTools이라는 패키지를 활용해서 Cronbach's alpha 값을 알아보겠습니다.
# semTools패키지 설치 및 실행
install.packages("semTools")
library(semTools)
#신뢰도 확인
reliability(fit)맨위 alpha 라고 나와있는 수치가 크론바흐 알파이며, 맨밑에 avevar이 ave수치 입니다.
Visual Textual Speed
alpha 0.6261171 0.8827069 0.6884550
omega 0.6253180 0.8851754 0.6877600
omega2 0.6253180 0.8851754 0.6877600
omega3 0.6120052 0.8850608 0.6858417
avevar 0.3705589 0.7210163 0.4244883AVE 값이 0.5 이상인 경우, 해당 요인의 집중타당도가 있다고 판단할 수 있습니다. 그러면 변수들이 해당 요인과 관련성이 높다고 볼 수 있으며, 동일한 구성 개념을 측정하고 있다고 할 수 있습니다.
4) 판별타당도
판별 타당도 (discriminant validity)는 다른 구성 개념을 측정하는 변수들이 서로 낮은 관련성을 보이는지 확인합니다. 판별 타당도를 평가하려면 요인 상관 행렬을 검토하고 각 요인의 평균 추출된 분산 (AVE)를 사용합니다.
#판별타당도 평가
cor_vars <- inspect(fit, 'cor.lv')
sqr_ave <- as.data.frame(sqrt(reliability(fit)[5,-4]))
colnames(sqr_ave) <- "AVE의 제곱근"
cbind(cor_vars, sqr_ave)코드를 실행하면 다음과 같은 결과가 출력됩니다.
Visual Textual Speed AVE의 제곱근
Visual 1.0000000 0.4585093 0.4705345 0.6087355
Textual 0.4585093 1.0000000 0.2829847 0.8491268
Speed 0.4705345 0.2829847 1.0000000 0.6515277분석결과를 살펴보면 AVE의 제곱근 값이 다른 변수간 상관계수보다 높은것으로 나타나서 판별타당도는 확보되었습니다.
4. R을 활용한 구조방정식 실습
1) 모형피팅
구조방정식을 분석하기 위해서는 구조방정식 모형을 설정해줘야합니다.
# 구조 모형 설정
SEM.model <- '
# measurement model
Visual =~ x1 + x2 + x3
Textual =~ x4 + x5 + x6
Speed =~ x7 + x8 + x9
# regressions
Speed=~Textual
Visual=~Textual+Speed
'위 코드를 입력하면 아래처럼 모형을 짜는것과 같습니다.
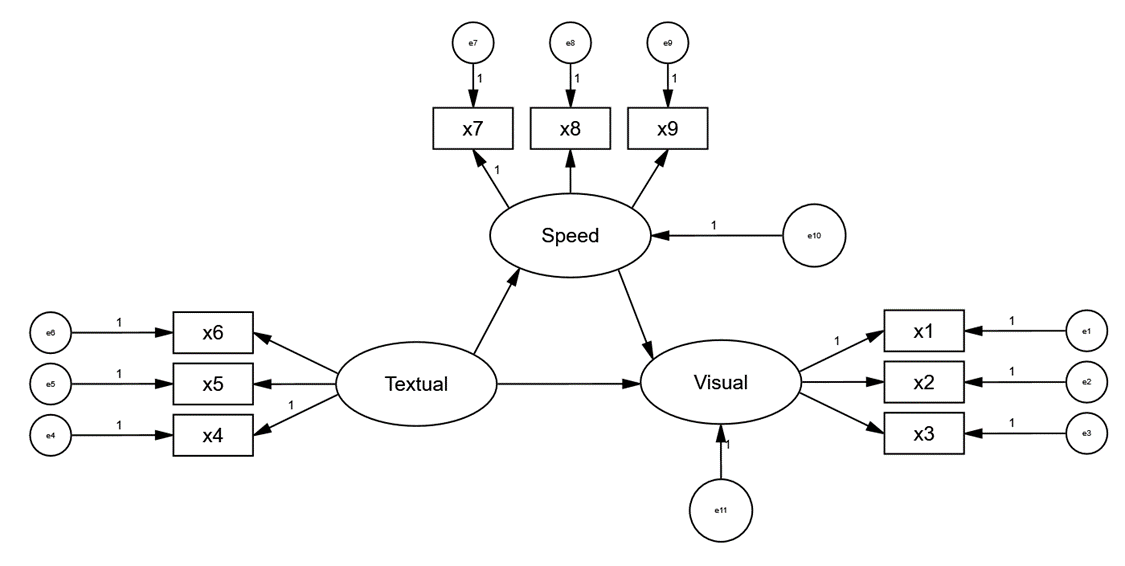
모형을 설정해줬으면 피팅해주고 결과를 살펴봅니다.
모형적합도를 살펴보는 방법은 위에 나와있는 방법과 같습니다.
# 모형 피팅
fit <- sem(SEM.model, data=HolzingerSwineford1939)
# 결과 살펴보기
summary(fit)2) 결과확인
서머리한 결과는 너무 깁니다...
lavaan 0.6-11 ended normally after 35 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 21
Number of observations 301
Model Test User Model:
Test statistic 85.306
Degrees of freedom 24
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
Visual =~
x1 1.000
x2 0.553 0.100 5.554 0.000
x3 0.729 0.109 6.685 0.000
Textual =~
x4 1.000
x5 1.113 0.065 17.014 0.000
x6 0.926 0.055 16.703 0.000
Speed =~
x7 1.000
x8 1.180 0.165 7.152 0.000
x9 1.082 0.151 7.155 0.000
Textual 0.138 0.138 1.002 0.316
Visual =~
Textual 0.460 0.108 4.237 0.000
Speed 0.324 0.071 4.581 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 0.549 0.114 4.833 0.000
.x2 1.134 0.102 11.146 0.000
.x3 0.844 0.091 9.317 0.000
.x4 0.371 0.048 7.778 0.000
.x5 0.446 0.058 7.642 0.000
.x6 0.356 0.043 8.277 0.000
.x7 0.799 0.081 9.823 0.000
.x8 0.488 0.074 6.573 0.000
.x9 0.566 0.071 8.003 0.000
Visual 0.809 0.145 5.564 0.000
.Textual 0.768 0.096 8.016 0.000
.Speed 0.299 0.071 4.237 0.000Subset기능을 확인해서 결과를 확인해봅시다.
subset(standardizedSolution(fit2),
standardizedSolution(fit2)[2]== "=~")확인 결과, Textual가 Visual로 가는 경로와 Speed가 Visual로 가는 경로의 p값이 .05보다 낮게 나타났습니다.
lhs op rhs est.std se z pvalue ci.lower ci.upper
1 Visual =~ x1 0.772 0.055 14.041 0.000 0.664 0.880
2 Visual =~ x2 0.424 0.060 7.105 0.000 0.307 0.540
3 Visual =~ x3 0.581 0.055 10.539 0.000 0.473 0.689
4 Textual =~ x4 0.852 0.023 37.776 0.000 0.807 0.896
5 Textual =~ x5 0.855 0.022 38.273 0.000 0.811 0.899
6 Textual =~ x6 0.838 0.023 35.881 0.000 0.792 0.884
7 Speed =~ x7 0.570 0.053 10.714 0.000 0.465 0.674
8 Speed =~ x8 0.723 0.051 14.309 0.000 0.624 0.822
9 Speed =~ x9 0.665 0.051 13.015 0.000 0.565 0.765
10 Speed =~ Textual 0.086 0.086 1.010 0.313 -0.081 0.254
11 Visual =~ Textual 0.418 0.082 5.083 0.000 0.257 0.579
12 Visual =~ Speed 0.471 0.073 6.461 0.000 0.328 0.613
'통계 > R' 카테고리의 다른 글
| R에서 결측치 처리하기 (1) | 2023.04.13 |
|---|---|
| R에서 Markdown 사용하기 (0) | 2023.04.04 |
| R에서 다중회귀분석하는 방법 (0) | 2023.03.23 |
| R에서 데이터 변수 위치 바꾸는 법(데이터 프레임의 컬럼 위치 변경) (0) | 2023.03.23 |
| R에서 컴퓨터를 끄는 방법 (0) | 2023.03.22 |







최근댓글