왜도와 첨도는 데이터의 분포 형태를 나타내는 중요한 통계량입니다. 이를 통해 데이터의 비대칭성과 뾰족함을 평가할 수 있습니다. 이해하면 데이터를 더 깊게 분석하는 데 도움이 됩니다

목차
- 왜도와 첨도의 정의: 기본 개념 소개
- 왜도의 해석: 분포의 비대칭성 파악하기
- 첨도와 분포의 뾰족함: 어떻게 분포의 봉우리를 측정하는가?
- 왜도와 첨도의 계산: 수식과 예제를 통한 이해
- 분포의 형태와 왜도, 첨도: 정규분포와 비교하기
- 왜도와 첨도의 실제 응용: 실세계 예제로의 적용
- 왜도와 첨도의 중요성: 왜 이러한 통계량을 사용하는가?
- 왜도와 첨도의 한계: 주의할 점 및 제한 사항
1. 왜도와 첨도의 정의: 기본 개념 소개
왜도와 첨도는 통계학에서 확률 분포의 모양을 설명하는 데 사용되는 두 개의 중요한 척도입니다.
- 왜도 (Skewness): 분포의 비대칭도를 나타냅니다. 왜도가 0인 경우 분포는 완벽하게 대칭입니다. 양수인 경우 분포는 오른쪽으로 기울어지며, 음수인 경우 왼쪽으로 기울어집니다.
- 첨도 (Kurtosis): 분포의 뾰족함을 나타냅니다. 첨도가 0인 경우 정규 분포와 유사한 뾰족함을 보입니다. 양수인 경우 뾰족하며, 음수인 경우 평평합니다.
2. 왜도의 해석: 분포의 비대칭성 파악하기
왜도는 분포의 대칭성을 측정합니다.
양의 왜도: 데이터의 대부분이 평균 아래에 있음을 나타냅니다. 즉, 오른쪽 꼬리가 긴 분포입니다.
양의 왜도는 대부분의 데이터가 왼쪽에 위치하고 오른쪽 꼬리가 긴 형태를 보입니다. 이는 데이터의 대부분이 평균 값 아래에 있음을 의미합니다.

음의 왜도: 데이터의 대부분이 평균 위에 있음을 나타냅니다. 즉, 왼쪽 꼬리가 긴 분포입니다.
음의 왜도는 대부분의 데이터가 오른쪽에 위치하고 왼쪽 꼬리가 긴 형태를 보입니다. 이는 데이터의 대부분이 평균 값 위에 있음을 의미합니다.

3. 첨도와 분포의 뾰족함: 어떻게 분포의 봉우리를 측정하는가?
첨도는 분포의 봉우리 정도를 설명합니다.
높은 첨도: 뾰족한 분포, 데이터의 대부분이 평균 주위에 몰려 있습니다.
높은 첨도는 뾰족한 분포로, 중앙에 데이터가 집중되어 있으며 극단값이 더 많습니다.

낮은 첨도: 평평한 분포, 데이터가 평균 주위로 넓게 퍼져 있습니다.
낮은 첨도는 평평한 분포로, 중앙에 데이터가 덜 집중되어 있습니다.

4. 왜도와 첨도의 계산: 수식과 예제를 통한 이해
왜도와 첨도는 통계학적 수식을 통해 계산됩니다.

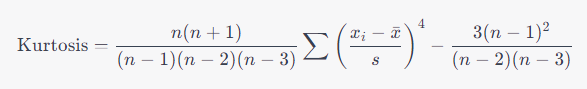
5. 분포의 형태와 왜도, 첨도: 정규분포와 비교하기
정규 분포는 왜도가 0이고 첨도가 3입니다. 따라서, 왜도와 첨도를 이용하여 분포가 정규분포와 얼마나 가까운지를 평가할 수 있습니다.
일반적으로 왜도는 절대값 3, 첨도는 절대값 10을 초과하지만 않으면 정규분포로 간주 합니다.
6. 왜도와 첨도의 실제 응용: 실세계 예제로의 적용
왜도와 첨도는 경제학, 금융, 과학 연구 등 다양한 분야에서 데이터 분포의 특성을 평가하는 데 사용됩니다. 예를 들어, 주식 시장의 수익률 분포를 분석할 때 왜도와 첨도를 사용하여 분포의 비대칭성과 뾰족함을 평가할 수 있습니다.
7. 왜도와 첨도의 중요성: 왜 이러한 통계량을 사용하는가?
왜도와 첨도는 데이터의 분포 형태를 이해하는 데 중요합니다. 이를 통해 데이터의 중심 경향성, 퍼짐 정도, 그리고 꼬리의 길이와 뾰족함을 파악할 수 있습니다. 이 정보는 데이터의 특성을 정확히 이해하고, 예측 모델링 및 의사 결정에 중요한 역할을 합니다.
8. 왜도와 첨도의 한계: 주의할 점 및 제한 사항
왜도와 첨도는 분포의 특성을 나타내는 척도이지만, 혼자서는 분포의 전체적인 모양을 완전히 설명하지 못합니다. 따라서, 다른 통계량과 함께 사용하는 것이 좋습니다. 또한, 큰 표본에서는 왜도와 첨도의 값이 안정적이지만, 작은 표본에서는 변동성이 클 수 있으므로 주의가 필요합니다.
| 아래 포스팅도 참고해 보세요! ▶ F값보고 p값 계산하는 법 ▶ 회귀분석 수치해석 및 의미 ▶ 로지스틱 회귀분석 이해하기 ▶ 이론적 배경 쓰는 법 |
'통계 > 통계이론' 카테고리의 다른 글
| AHP분석에 대해 알아보자 (0) | 2023.09.25 |
|---|---|
| 카이제곱 분석 이해하기 (2) | 2023.09.23 |
| ANOVA 사후검증의 종류와 특징 (0) | 2023.09.14 |
| F값보고 p값 계산하는 법 (0) | 2023.09.08 |
| 회귀분석 유형과 해석방법 (0) | 2023.07.27 |








최근댓글